ÔN TẬP CHƯƠNG II
Đại số và Giải tích 11
I. Kiến thức trọng tâm cần nắm
- Quy tắc cộng, quy tắc nhân và cách vận dụng;
- Khái niệm hoán vị, chỉnh hợp, tổ hợp và cách tính số phần tử của các đại lượng đó;
- Khai triển biểu thức theo công thứcNewton; vận dụng để tìm số hạng hoặc hệ số của số hạng theo yêu cầu;
- Khái niệm phép thử, biến cố (các loại: biến cố chắc chắn, biến cố không, biến cố đối, biến cố xung khắc, biến cố độc lập), hợp và giao của các biến cố; xác suất (cố điển).
II. Bài tập
A. Quy tắc cộng, quy tắc nhân, hoán vị, chỉnh hợp, tổ hợp
Bài 1: Từ các chữ số 1, 2, 3, 4, 5 có thể lập được mấy số tự nhiên có năm chữ số:
a) các chữ số tùy ý;
b) các chữ số khác nhau;
c) các chữ số khác nhau và chữ số hàng trăm là số chẵn;
d) bé hơn 54321 và các chữ số khác nhau.
Bài 2: Từ các chữ số 1, 2, 3, 4, 5, 6, 7 có thể lập được mấy số tự nhiên có năm chữ số:
a) các chữ số tùy ý;
b) các chữ số khác nhau;
c) các chữ số khác nhau và chữ số hàng nghìn là số lẻ;
d) có 3 chữ số giống nhau và các chữ số còn lại khác nhau.
Bài 3: Có hai chuồng thỏ, chuồng I nhốt 4 thỏ cái và 5 thỏ đực, chuồng II nhốt 5 thỏ cái và 3 thỏ đực. Hỏi có mấy cách bắt một lần 4 con thỏ từ một trong hai chuồng đã cho sao cho mỗi lần bắt:
a) các con thỏ tùy ý (không phân biệt dực, cái);
b) chỉ có 2 con thỏ đực;
c) có ít nhất 2 con thỏ đực;
d) số thỏ cái nhiều hơn số thỏ đực.
B. Khai triển biểu thức theo công thức Newton
Bài 4: Khai triển và rút gọn các biểu thức sau:
a)  b)
b) 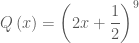
Bài 5: Tìm hệ số của số hạng chứa  trong khai triển và rút gọn biểu thức
trong khai triển và rút gọn biểu thức  .
. Bài 6: Tính tổng các hệ số của số hạng chứa  trong khai triển và rút gọn biểu thức
trong khai triển và rút gọn biểu thức  .
. C. Xác suất của biến cố
Bài 7: Xét phép thử: “Gieo ngẫu nhiên 3 đồng xu một lần”. Ký hiệu “S”, “N” để chỉ mặt xuất hiện là mặt có hình và có số (theo thứ tự đó).
a) Xác định không gian mẫu (liệt kê các phần tử);
b) Tính xác suất của các biến cố:
A: “Có 2 lần đồng xu xuất hiện mặt sấp”;
B: “Có ít nhất một lần đồng xu xuất hiện mặt sấp”;
C: “Lần thứ nhất đồng xu xuất hiện mặt sấp”
D: “Lần thứ ba đồng xu xuất hiện mặt sấp”
c) A, B có phải là biến cố xung khắc không ? Vì sao ?
d) Chứng tỏ C, D là hai biến cố độc lập.
Bài 8: Một hộp có chứa 3 viên bi xanh, 5 viên bi đỏ và 4 viên bi vàng. Xét phép thử: “Lấy ngẫu nhiên một lần 3 viên bi từ hộp”.
a) Tính số phần tử của không gian mẫu;
b) Tính xác suất của các biến cố sau:
A: “3 viên bi lấy ra cùng màu”;
B: “Trong 3 viên bi lấy ra, có 1 viên bi vàng”;
C: “Trong 3 viên bi lấy ra, có ít nhất 1 viên bi vàng”;
D: “Trong 3 viên bi lấy ra, ít nhất 1 viên bi vàng và 1 viên bi đỏ”.
ĐỀ KIỂM TRA CUỐI CHƯƠNG
(THAM KHẢO)
Câu 1: (3 điểm) Từ các chữ số 0, 1, 2, 3 có thể lập được mấy số tự nhiên có 3 chữ số
a) các chữ số khác nhau;
b) là số lẻ và có 2 chữ số giống nhau.
Câu 2: (3 điểm) Khai triển và rút gọn biểu thức  .
. Tính tổng các hệ số của số hạng chứa 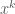 với
với 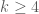 .
. Câu 3: (4 điểm) Một hộp có 3 viên bi: 1 viên bi vàng, 1 viên bi đỏ và 1 viên bi xanh. Xét phép thử: “Gieo ngẫu nhiên một đồng xu sau đó bốc lần lượt hai viên bi từ hộp”.
Ký hiệu “S”, “N” để chỉ mặt xuất hiện là mặt có hình và có số (theo thứ tự đó); Ký hiệu: “đ”, “x”, “v” để chỉ viên bi bốc được lần lượt có màu đỏ, xanh, vàng.
a) Mô tả không gian mẫu (liệt kê các phần tử);
b) Tính xác suất của các biến cố:
A: “Đồng xu xuất hiện mặt sấp”;
B: “Viên bi bốc trước có màu đỏ”;
C: “Bốc được 2 viên bi màu xanh và đỏ”.
c) Xét xem trong A, B, C hai biến cố nào là biến cố độc lập ?
:
(1)
. (2)
xẩy ra khi và chỉ khi
.
, ta có:
(Vì
.
.
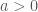 nên
nên  . Áp dụng BĐT (2) cho hai số này ta được:
. Áp dụng BĐT (2) cho hai số này ta được: .
..
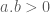 nên
nên  . Áp dụng BĐT (2) cho hai số này ta được:
. Áp dụng BĐT (2) cho hai số này ta được: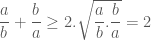 .
.ta có:
.
 nên phần còn lại phải biểu diễn thành thừa số của
nên phần còn lại phải biểu diễn thành thừa số của 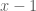 . Vậy ta phải viết lại vế trái như sau:
. Vậy ta phải viết lại vế trái như sau: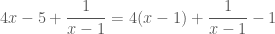 (*)
(*)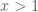 nên
nên  .
. , ta có:
, ta có:
 . (**)
. (**) .
. (đpcm)
(đpcm)

 (do
(do  )
) .
. . (3)
. (3)![x\in [1; 5] x\in [1; 5]](http://s0.wp.com/latex.php?latex=x%5Cin+%5B1%3B+5%5D&bg=ffffff&fg=4e4e4e&s=0) thì
thì 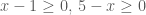 . Vậy áp dụng BĐT (3) cho hai số không âm này ta có:
. Vậy áp dụng BĐT (3) cho hai số không âm này ta có: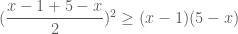
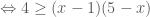 . (đpcm)
. (đpcm) .
..
, ta có:
.
.
.








